Likelihood vs Probability
Likelihood Definition (Wikipedia) : In statistics, the likelihood function expresses how probable a given set of observations is for different values of statistical parameters. It is equal to the joint probability distribution of the random sample evaluated at the given observations, and it is, thus, solely a functoin of paramters that index the family of those probability distributions.
1. What is Likelihood?
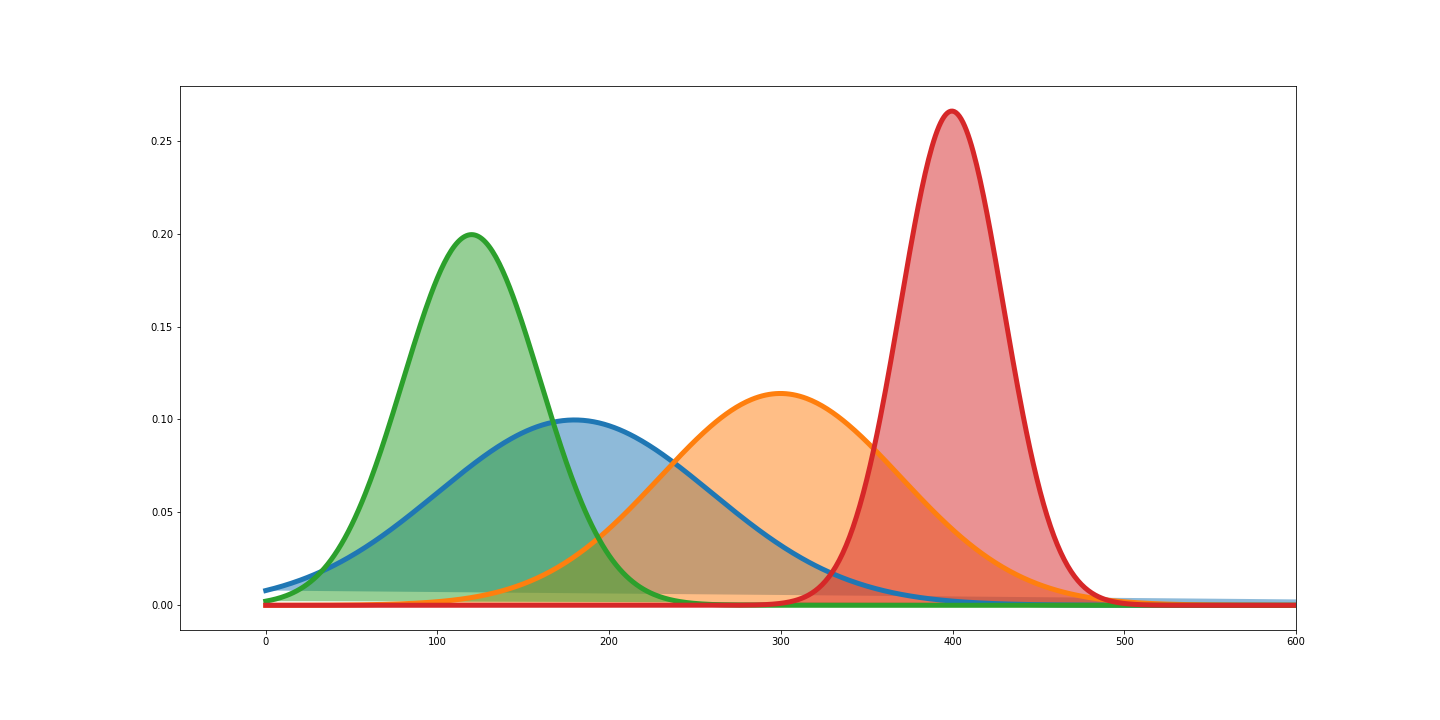
Likelihoods are the y-axis values for fixed data points with distribution that can be moved, as the following;
$$\mathcal{L}(\theta | x) = \mathcal{L}(distribution | data)$$
Whereas, Probabilities are the areas under a fixed distribution.
$$P(data | distribution)$$
If we find the maximum y-axis value for fixed data points by moving the distribution, we find the optimal distribution for the fixed data.
Therefore, we can use the likelihood function to fit a optimal distribution on the fixed data by finding maximum likelihood estimator.
2. Maximum Likelihood?
To find the maximum likelihood estimator, we might find a function for likelihoods given fixed data points, and take a derivative for the function, and set the derivatives as 0.
Example 1: Exponential distribution
The Probability Density Function of Exponential Distribution is defined as the following;
$$f(x; \lambda) = \lambda e ^ {- \lambda x} \qquad if \qquad x \geq 0$$
Otherwise,
$$f(x; \lambda) = 0$$
for $\lambda >0$, which is rate parameter of the distribution.
Hence, the exponential distribution will be shaped by the $\lambda$.
Therefore, we want to find the maximum likelihood of $\lambda$ for given data.
$$\mathcal{L}(\lambda | x_1, x_2, … , x_n) = \mathcal{L}(\lambda | x_1)\mathcal{L}(\lambda | x_2)…\mathcal{L}(\lambda | x_n) $$
$$= \lambda e ^ {- \lambda x_1}\lambda e ^ {- \lambda x_2}…\lambda e ^ {- \lambda x_n} \\ = \lambda^{n}(e ^ {-\lambda (x_1 + x_2 + … + x_n)})$$
Now, take a derivative for the likelihood function to find maximum likelihood estimator of $\lambda$.
$$ \frac{d}{d\lambda} \mathcal{L}(\lambda | x_1, x_2, … , x_n) = \frac{d}{d\lambda} \lambda^{n} (e ^ {-\lambda * (x_1 + x_2 + … + x_n)})$$
Before derivitaves, there is more easier way to differentiate this function, which is to take a lograithm on the function.
Take a logarithm on the likelihood function, then this becomes the log likelihood function.
$$log (\mathcal{L}(\lambda | x_1, x_2, … , x_n)) = log(\mathcal{L}(\lambda | x_1)\mathcal{L}(\lambda | x_2)…\mathcal{L}(\lambda | x_n))
$$
Which makes easier differentiate the function.
$$ \frac{d}{d\lambda} log(\mathcal{L}(\lambda | x_1, x_2, … , x_n)) = \frac{d}{d\lambda} log(\lambda^{n}(e ^ {-\lambda * (x_1 + x_2 + … + x_n)}))$$
$$= \frac{d}{d\lambda} (log(\lambda ^ {n}) + log(\lambda^{n}(e ^ {-\lambda * (x_1 + x_2 + … + x_n)}))) \\ = \frac{d}{d\lambda} (n log(\lambda) - \lambda (x_1 + x_2 + … + x_n)) \\ = n \frac{1}{\lambda} - (x_1 + x_2 + … + x_n)$$
Set this as zero,
$$n \frac{1}{\lambda} - (x_1 + x_2 + … + x_n) = 0$$
Which gives you,
$$ \frac{(x_1 + x_2 + … + x_n)}{n} = \mu = \frac{1}{\lambda}$$
Therefore, the maximum likelihood estimator of $\lambda$ is
$$\lambda = \frac{1}{\mu}$$.
And, this connects to the concept of the maximum entropy probability distribution.
“The exponential distribution is the maximum entropy distribution among all continuous distribution supported in $[0, \infty]$ that have a specified mean of $\frac{1}{\lambda}$”
Example 2: Normal Distribution
In normal distribution (often called Gaussian distribution), the mean $\mu$ and the variance $\sigma^2$ will be the parameter that the determines how the normal distribution looks like. With $\mu$ and $\sigma^2$, we will find the maximum likelihood estimator for the normal distribution given fixed data.
The PDF of normal distribution is defined as,
$$f(x|\mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$
The Likelihood of $\mu$ and $\sigma$ for normal distribution will be,
$$\mathcal{L}(\mu, \sigma|x_1, x_2, … , x_n) = \mathcal{L}(\mu, \sigma^2|x_1)\mathcal{L}(\mu, \sigma^2|x_2)…\mathcal{L}(\mu, \sigma^2|x_n)$$
$$= \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x_1-\mu)^2}{2\sigma^2}}\frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x_2-\mu)^2}{2\sigma^2}}…\frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x_n-\mu)^2}{2\sigma^2}}$$
Before take a derivatives, we take a log on the function as done in exponential.
$$log(\mathcal{L}(\mu, \sigma|x_1, x_2, … , x_n))= log(\frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x_1-\mu)^2}{2\sigma^2}}\frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x_2-\mu)^2}{2\sigma^2}}…\frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x_n-\mu)^2}{2\sigma^2}})$$
By simplifying the log likelihood function with the properties of logarithm,
$$= \sum_{i=1}^{n}(log(\frac{1}{\sqrt{2\pi\sigma^2}}) -\frac{(x_i-\mu)^2}{2\sigma^2}) \\ = -\frac{n}{2}log(2\pi) - nlog(\sigma) - \sum_{i=1}^{n}\frac{(x_i-\mu)^2}{2\sigma^2}$$
Now, take the derivative with respect to the $\mu$,
$$\frac{\partial}{\partial \mu} log(\mathcal{L}(\mu, \sigma|x_1, x_2, … , x_n)) \\ = 0 - 0 + \sum_{i=1}^{n} \frac{(x_i-\mu)}{\sigma^2} \\ = \sum_{i=1}^{n} \frac{x_i}{\sigma^2} - n\mu$$
Set this as 0,
$$\sum_{i=1}^{n} \frac{x_i}{\sigma^2} - n\mu = 0$$
Since $\sigma^2$ is constant here,
$$ \sum_{i=1}^{n} x_i = n\mu$$
Hence,
$$\mu = \sum_{i=1}^{n} x_i / n$$
which is the mean of the measurements.
Taking derivative with respect to the $\sigma$,
$$\frac{\partial}{\partial \sigma} log(\mathcal{L}(\mu, \sigma|x_1, x_2, … , x_n)) = \frac{\partial}{\partial \sigma} (-\frac{n}{2}log(2\pi) - nlog(\sigma) - \sum_{i=1}^{n}\frac{(x_i-\mu)^2}{2\sigma^2}) \\ = 0 - \frac{n}{\sigma} + \sum_{i=1}^{n} \frac{(x_i - \mu)^2}{\sigma^3}$$
Set this as 0,
$$0 - \frac{n}{\sigma} + \sum_{i=1}^{n} \frac{(x_i - \mu)^2}{\sigma^3} = 0 \\ n = \sum_{i=1}^{n} \frac{(x_i - \mu)^2}{\sigma^2} \\ \sigma^2 = \sum_{i=1}^{n} \frac{(x_i - \mu)^2}{n} \\ \sigma = \sum_{i=1}^{n} \sqrt{\frac{(x_i - \mu)^2}{n}}$$
which is the standard deviation of the measurements.
In conclusion,
the mean of the data is the maximum likelihood estimate for where the center of the distribution should be,
the standard deviation of the data is the maximum likelihood estimate for how wide the curve of the distribution should be.
This also connects to the maximum entropy probability distribution as the following;
The normal distribution has maximum entropy among all real-valued distribution supported on $(-\infty, \infty)$ with a specified variance $\sigma^2$.
Reference:
Likelihood(wiki)
Maximum Entropy Probability Distribution(wiki)
Related to Likelihood for distributions (StatQuest with Josh Starmer)