Monty Hall Problem with Bayes’ Theorem
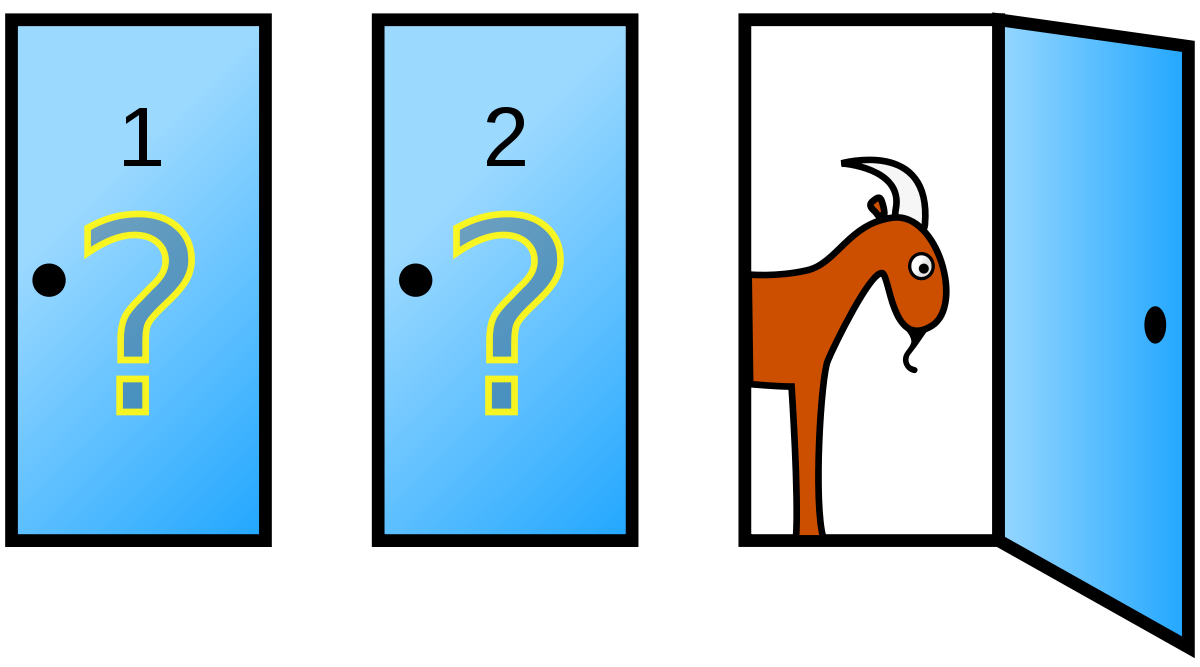
Monty Hall Problem is a famous probability problem based on the TV show, “Let’s make a Deal.”
Suppose that you are a contestant and are asked to choose a door among 3 doors, which contains 1 car and 2 goats. If you choose a door that is car behind the door, then you win the prize.
Let C = car behind the door $i$, and D = open door $j$.
Here, we can formulate the probability for the car behind the door as the following:
$$P(C=1) = 1/3 \qquad P(C = 2) = 1/3 \qquad P(C = 3) = 1/3$$
Let’s say you pick the door 1, and host pick one of door 2 or 3, which goat behind the door. You now have a choice whether you stick with the originally chosen door and you switch.
Suppose the host choose the door 3, given that a goat is behind the door 3.
The trick of the probablity here is that the host knows which door has a car behind it and will never open the door. Then, there’s 50-50 chances that one of the two doors, which is not the door that host opens, has a car behind it.
The probability of the door that is chosen by the host, given that the car behind the door, is zero, since the host never pick the door that has a car,
the probability of the door that is chosen by the contestant, given that the car behind the door, is a half, since it is the half probability,
and the probability of the door that is not chosen by the host, given that the car behind the door, is one, because the host never pick the door that has a car and the door that the contestant chose, there’s only one door left.
Then, the likelihood will be
$$P(D = 3 | C = 1) = 1/2 \qquad P(D = 3 | C = 2) = 1 \qquad P(D = 3 | C = 3) = 0 $$
Now, the formula of Bayes Theorem is the following:
$$P(C = i | D = 3) = \frac{P(D = 3 | C = i)P(C = i)}{P(D = 3)}$$
It is easy to answer that the probability for $P(D = 3)$ is $\frac{1}{2}$, because you already choose door 1, and the host will choose one of the rest 2 doors. However, we can calculate the marginal probability for $P(D = 3)$ as the following.
$$P(D = 3) = \sum_{i=1}^{3} P(C = i, D = 3) = \sum_{i=1}^{3} P(D = 3 | C = i)P(C = i) = \\ P(D = 3 | C = 1)P(C = 1) + P(D = 3 | C = 2)P(C = 2) + P(D = 3 | C = 3)P(C = 3) = \\ \frac{1}{3} \times \frac{1}{2} + \frac{1}{3} \times 1 + \frac{1}{3} \times 0 = \frac{1}{2}$$
Now, let’s calculate the posterior probability in the Bayes Theorem, which is the probability of the door has a car behind it, given the door 3 has opened.
$$P(C = 1 | D = 3) = \frac{P(D = 3 |C = 1)P(C = 1)}{P(D = 3)} = \frac{\frac{1}{2} \times \frac{1}{3}}{\frac{1}{2}} = \frac{1}{3}$$
$$P(C = 2 | D = 3) = \frac{P(D = 3 |C = 2)P(C = 2)}{P(D = 3)} = \frac{1 \times \frac{1}{3}}{\frac{1}{2}} = \frac{2}{3}$$
$$P(C = 3 | D = 3) = \frac{P(D = 3 |C = 3)P(C = 3)}{P(D = 3)} = \frac{0 \times \frac{1}{3}}{\frac{1}{2}} = 0$$
Therefore, as a contestant, you have to switch your choice to door 2 that has more probability than the door you chose at the first time.