
Deep Neural Networks
Simple Intro to DNN
DNN(Deep Neural Networks) is a deep structured model of ANN(Artificial Neural Networks), which is a type of machine learning inspired by biological neural networks. DNN is used and applied widely in many fields such as computer vision, speech recognition, natural language processing, and bioinformatics.
For my understand, ANN is to stack many models with various weights and biases such as logistic regression models, and DNN is a complex body that consist of huge amount of models. Therefore, some DNN model has more than 20 million parameters such as Xception invented from Google.
As any other complexity in this world brings about problems, DNN has some problems that has to be solved. DNN suffers slow computational time because it has more than millions parameters to learn. And it also suffers the vanishing/exploding gradients problems. Because it has all the different models, which are neurons, with all the different weights and biases, the gradients of some neurons to update each weights and biases will be too small or too large. In this case, we say that the neurons with too small or too large gradients are dead neurons.
There are many approches to alleviate those problems such as dropout, initializer, or batch normalization.
I am going to disscuss about efficient optimizers rather than Stochastic Gradient Descent, which is one of ways for those difficulties.
SGD (Stochastic Gradient Descent)
Let’s begin with talking about what the SGD is.
Regular Gradient Descent is to simply updates the weights by calculating and subtracting the gradient of cost function with regards to the weights to reach the global optimum so that we can minimize our cost function.
Definition:
$$\theta \leftarrow \theta - \eta\Delta_{\theta}\mathcal{J}(\theta)$$
The formula in the definition is to update the weights by subtracting or adding the gradients of cost function to take small steps down the slope.
So SGD does not care about the previous weights or gradients, but it only cares about current weights and gradients. This is where the Momentum optimization is introduced.
SGD with Momentum optimization
SGD with Momentum Optimization is simply added some vector in the process of SGD, which is called momentum vector.
Definition:
$$\mathcal{m} \leftarrow \beta\mathcal{m} - \eta\Delta_{\theta} \mathcal{J}(\theta)$$
$$\theta \leftarrow \theta + \mathcal{m}$$
We update the weight by updating the momenum vector as above. Let’s imagine that we starts with the first initialized weights at the first iteration. The moment vector, $\mathcal{m}$, is started with zero, then the weights, $\theta$, will be just updated by the gradients as Gradient Decsent does. At the second iteration, the momentum vector is the gradients calculated at the first iteration. We are updating the gradients of the first iteration, which is momentum vector, by subtracting or adding the gradients at the current step, and adding the updated the gradients or the momentum vector. At the third iteration, the momentum vector would be the updated momentum vector at the second iteration, which is calculated by the first gradients. We update the wegiths by updating and adding the momentum vector.
To prevent the momentum vector growing too large or too small, we slightly reduced the value by a hyperparameter, $\beta$, which is called momentum. If the momentum, $\beta = 0$, then it’s the same as SGD. The typical value of momentum is 0.9.
Nesterov Accelerated Gradient
A new Momentum optimization is introduced, which is called Nesterov Accelerated Gradient. In the original Momentum Optimization, we update the momenum vector at the local position of the current weight; however, in NAG optimization, we update the momentum vector with the gradient that is measured at $\theta + \beta\mathcal{m}$.
Definition:
$$\mathcal{m} \leftarrow \beta\mathcal{m} - \eta\Delta_{\theta}\mathcal{J}(\theta + \beta\mathcal{m})$$
$$\theta \leftarrow \theta + \mathcal{m}$$
Since this gradient has the information of both of the weight and the previous momentum, this will help update the gradient more accurate, improve the directions to the optimum, and eventually converges faster.
AdaGrad
AdaGrad is the different version of gradient descent optimization than the momentum based optimization. It’s scaling down the gradient vector by dividing some factors measured along the steepness of the gradient.
Definition:
$$s \leftarrow s + \Delta_{\theta}\mathcal{J}(\theta)\otimes\Delta_{\theta}\mathcal{J}(\theta)$$
$$\theta \leftarrow \theta - \eta\Delta_{\theta}\mathcal{J}(\theta)\oslash\sqrt{s + \epsilon}$$
In the first step, we update the factor s by adding the element-wise multiplication of the gradient elements, that is the square of the gradients. It will be the same as $s_{i} \leftarrow + (\partial \mathcal{J}(\theta)/\partial \Theta_{i})^2$ for each element $s_{i}$. The vector, s, will accumulate the squares of the partial derivative of the cost function with regards to parameter $\Theta_{i}$. Therefore, if the gradient of the cost function is big, the factor s will get larger and larger at each iteration.
In the second step, the gradient of the cost function will be divided by the square root of the factor that is updated with the square of the gradients in the first step. The $\epsilon$ is the smoothing term to prevent dividing by zero, if the factor, s, is zero.
To sum up, if the direction to the global optimum is steep at the $i^{th}$ iteration, then the factor gets larger and so the term, $\eta\Delta_{\theta}\mathcal{J}(\theta)\oslash\sqrt{s + \epsilon}$, will be smaller. However, because it’s scaling down the gradient quickly at each iterations, when it’s reaching to the optimum, the gradient will be too small.
RMSProp
Since AdaGrad is scaling down the gradients too quickly, a new hyperparameter, $\beta$, is applied into the first formula of AdaGrad to somehow reduce the speed of scaling down.
Definition:
$$\mathcal{s} \leftarrow \beta\mathcal{s} + (1-\beta)\Delta_{\theta}\mathcal{J}(\theta)\otimes\Delta_{\theta}\mathcal{J}(\theta)$$
$$\theta \leftarrow \theta - \eta\Delta_{\theta}\mathcal{J}(\theta)\oslash\sqrt{s + \epsilon}$$
The hyperparameter, $\beta$, is called decay rate, and the typical value is 0.9.
Adam
Adam stands for adaptive moment estimation. It is from the ideas of momentum and RMSProp. Adam is a well-performed optimization algorithm in most cases.
Definition:
$$1. \mathcal{m} \leftarrow \beta_{1}\mathcal{m} - (1-\beta_{1})\Delta_{\theta}\mathcal{J}(\theta)$$
$$2. \mathcal{s} \leftarrow \beta_{2}\mathcal{s} + (1-\beta_{2})\Delta_{\theta}\mathcal{J}(\theta) \otimes \Delta_{\theta}\mathcal{J}(\theta)$$
$$3. \hat{\mathcal{m}} \leftarrow \frac{m}{1-\beta_{1}^{t}}$$
$$4. \hat{\mathcal{s}} \leftarrow \frac{s}{1-beta_{2}^{t}}$$
$$5. \theta \leftarrow \theta + \eta\hat{\mathcal{m}}\oslash\sqrt{\hat{\mathcal{s}} + \epsilon}$$
The step 1 is to update the momentum vector with the idea of RMSProp, which is reducing the the speed of scaling the momentum vector by weighting each terms with the decay rate, $\beta_{1}$
The step 2 is to update the factor s, which is similar to the factor s in RMSProp.
The step 3 and 4 is to reweight the momentum vetor and the factor s by each decay rate. Because the momentum vector and the factor s will be initialized at 0, the $\mathcal{m}$ and $\mathcal{s}$ will be boosted from the beginning of training.
The step 5 is final step to update the weight, $\theta$, with all the parameters of $\mathcal{m}$ and $\mathcal{s}$ from above steps.
The typlical value of momentum decay rate, $\beta_{1}$, is 0.9, and the scailing decay hyperparameter, $\beta_{2}$, is set to 0.999.
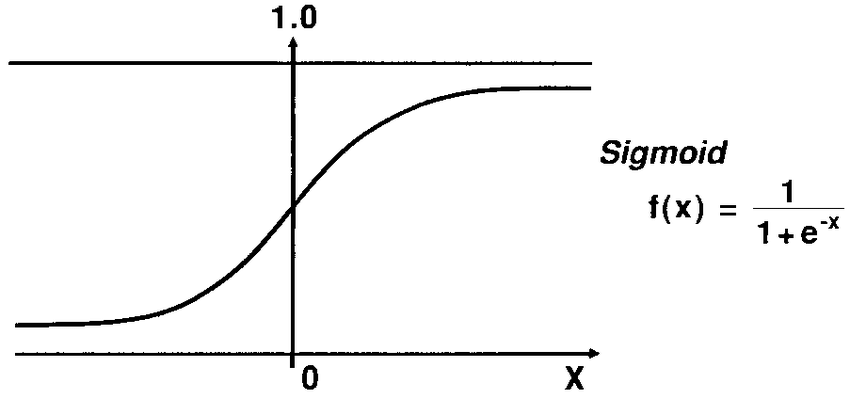
![[logistic]](/2020/01/02/logistic/LogisticResult1.png)
![[logistic]](/2020/01/02/logistic/LogisticResult2-1.png)
![[logistic]](/2020/01/02/logistic/LogisticResult2-2.png)
![[logistic]](/2020/01/02/logistic/LogisticResult3.png)
![[logistic]](/2020/01/02/logistic/LogisticResult4-1.png)
![[logistic]](/2020/01/02/logistic/LogisticResult4-2.png)
![[logistic]](/2020/01/02/logistic/LogisticResult5.png)
![[logistic]](/2020/01/02/logistic/LogisticResult6.png)
![[logistic]](/2020/01/02/logistic/LogisticResult7.png)
![[table]](/2019/10/24/PCA/numlay.png)
![[table]](/2019/10/24/PCA/denomlay.png)
![[table]](/2019/10/16/AUROC/confusion.png)
![[table]](/2019/10/16/AUROC/target.png)
![[table]](/2019/10/16/AUROC/pred1CM.png)
![[table]](/2019/10/16/AUROC/pred3CM.png)
![[table]](/2019/10/16/AUROC/pred5CM.png)
![[table]](/2019/10/16/AUROC/pred7CM.png)
![[table]](/2019/10/16/AUROC/1.png)
![[table]](/2019/10/16/AUROC/2.png)
![[table]](/2019/10/16/AUROC/8.png)
![[table]](/2019/10/16/AUROC/3.png)
![[table]](/2019/10/16/AUROC/4.png)
![[table]](/2019/10/16/AUROC/5.png)
![[table]](/2019/10/16/AUROC/6.png)
![[table]](/2019/10/16/AUROC/7.png)

![[Reticulate]](/2019/10/07/Reticulate/dt1.png)
![[Reticulate]](/2019/10/07/Reticulate/dt2.png)
![[Reticulate]](/2019/10/07/Reticulate/dt3.png)
![[Reticulate]](/2019/10/07/Reticulate/dt4.png)
![[Reticulate]](/2019/10/07/Reticulate/dt5.png)
![[Reticulate]](/2019/10/07/Reticulate/dt6.png)
![[Reticulate]](/2019/10/07/Reticulate/pythonDec.png)
![[Reticulate]](/2019/10/07/Reticulate/pydt1.png)
![[Reticulate]](/2019/10/07/Reticulate/pydt2.png)
![[Reticulate]](/2019/10/07/Reticulate/pydt3.png)
![[Reticulate]](/2019/10/07/Reticulate/pydt4.png)
![[Reticulate]](/2019/10/07/Reticulate/pydt5.png)
![[Reticulate]](/2019/10/07/Reticulate/pydt6.png)
![[Reticulate]](/2019/10/07/Reticulate/pydt7.png)
![[Reticulate]](/2019/10/07/Reticulate/pydt8.png)
![[Reticulate]](/2019/10/07/Reticulate/pydt9.png)
![[Reticulate]](/2019/10/07/Reticulate/pythonDec2.png)
![[Reticulate]](/2019/10/07/Reticulate/pytoR.png)
![[Reticulate]](/2019/10/07/Reticulate/fromPythontoR-1.png)
![[Reticulate]](/2019/10/07/Reticulate/pytoR2.png)
![[Reticulate]](/2019/10/07/Reticulate/fromPythontoR-2.png)

![[table]](/2019/09/19/DecisionTree/image1.png)
![[table]](/2019/09/19/DecisionTree/image2.png)
![[table]](/2019/09/19/DecisionTree/image3.png)
![[table]](/2019/09/19/DecisionTree/Tree1.png)
![[table]](/2019/09/19/DecisionTree/Tree2.png)
![[table]](/2019/09/19/DecisionTree/Tree3.png)
![[table]](/2019/09/19/DecisionTree/table.png)
![[tree1]](/2019/09/19/DecisionTree/IntroductionDecisionTree-1.png)
![[tree1]](/2019/09/19/DecisionTree/IntroductionDecisionTree-2.png)
![[tree1]](/2019/09/19/DecisionTree/Prediction-1.png)
![[GP]](/2019/09/15/GaussianProcess/GP-1.png)
![[GP]](/2019/09/15/GaussianProcess/GP-2.png)
![[GP]](/2019/09/15/GaussianProcess/GP-3.png)
![[GP]](/2019/09/15/GaussianProcess/GP-5.png)

![[hist]](/2019/09/09/hist/histrogram-1.png)
![[hist]](/2019/09/09/hist/histrogram-2.png)
![[hist]](/2019/09/09/hist/histrogram-3.png)